Methods for the smooth functions in R

I have been asked recently by a colleague of mine how to extract the variance from a model estimated using adam() function from the smooth package in R. The problem was that that person started reading the source code of the forecast.adam() and got lost between the lines (this happens to me as well sometimes). Well, there is an easier solution, and in this post I want to summarise several methods that I have implemented in the smooth package for forecasting functions. In this post I will focus on the adam() function, although all of them work for es() and msarima() as well, and some of them work for other functions (at least as for now, for smooth v4.1.0). Also, some of them are mentioned in the Cheat sheet for adam() function of my monograph (available online).

Before I start, I have a short announcement. Kandrika Pritularga and I are planning to host the first online course on “Demand Forecasting with R” in November 2025. There are still some places left, so you can register via the Lancaster University shop. You can read about the course here.

The main methods

The adam class supports several methods that are used in other packages in R (for example, for the lm class). Here are they:

• forecast() and predict() – produce forecasts from the model. The former is preferred, the latter has a bit of limited functionality. See documentation to see what forecasts can be generated. This was also discussed in Chapter 18 of my monograph.
• fitted() – extracts the fitted values from the estimated object;
• residuals() – extracts the residuals of the model. These are values of \(e_t\), which differ depending on the error type of the model (see discussion here);
• rstandard() – returns standardised residuals, i.e. residuals divided by their standard deviation;
• rstudent() – studentised residuals, i.e. residuals that are divided by their standard deviation, dropping the impact of each specific observation on it. This helps in case of influential outliers.

An additional method was introduced in the greybox package, called actuals(), which allows extracting the actual values of the response variable. Another useful method is accuracy(), which returns a set of error measures using the measures() function of the greybox package for the provided model and the holdout values.

All the methods above can be used for model diagnostics and for forecasting (the main purpose of the package). Furthermore, the adam class supports several functions for working with coefficients of models, similar to how it is done in case of lm:

• coef() or coefficient() – extracts all the estimated coefficients in the model;
• vcov() – extracts the covariance matrix of parameters. This can be done either using Fisher Information or via a bootstrap (bootstrap=TRUE). In the latter case, the coefbootstrap() method is used to create bootstrapped time series, reapply the model and extract estimates of parameters;
• confint() – returns the confidence intervals for the estimated parameter. Relies on vcov() and the assumption of normality (CLT);
• summary() – returns the output of the model, containing the table with estimated parameters, their standard errors and confidence intervals.

Here is an example of an output from an ADAM ETS estimated using adam():

adamETSBJ <- adam(BJsales, h=10, holdout=TRUE)
summary(adamETSBJ, level=0.99)

The first line above estimates and selects the most appropriate ETS for the data, while the second one will create a summary with 99% confidence intervals, which should look like this:

Model estimated using adam() function: ETS(AAdN)
Response variable: BJsales
Distribution used in the estimation: Normal
Loss function type: likelihood; Loss function value: 241.1634
Coefficients:
      Estimate Std. Error Lower 0.5% Upper 99.5%  
alpha   0.8251     0.1975     0.3089      1.0000 *
beta    0.4780     0.3979     0.0000      0.8251  
phi     0.7823     0.2388     0.1584      1.0000 *
level 199.9314     3.6753   190.3279    209.5236 *
trend   0.2178     2.8416    -7.2073      7.6340  

Error standard deviation: 1.3848
Sample size: 140
Number of estimated parameters: 6
Number of degrees of freedom: 134
Information criteria:
     AIC     AICc      BIC     BICc 
494.3268 494.9584 511.9767 513.5372

How to read this output, is discussed in Section 16.3.

Multistep forecast errors

There are two methods that can be used as additional analytical tools for the estimated model. Their generics are implemented in the smooth package itself:

1. rmultistep() - extracts the multiple steps ahead in-sample forecast errors for the specified horizon. This means that the model produces the forecast of length h for every observation starting from the very first one, till the last one and then calculates forecast errors based on it. This is used in case of semiparametric and nonparametric prediction intervals, but can also be used for diagnostics (see, for example, Subsection 14.7.3);
2. multicov() - returns the covariance matrix of the h steps ahead forecast error. The diagonal of this matrix corresponds to the h steps ahead variance conditional on the in-sample information.

For the same model that we used in the previous section, we can extract and plot the multistep errors:

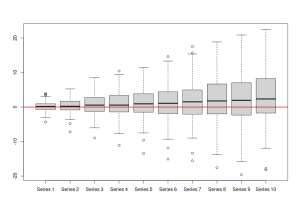
rmultistep(adamETSBJ, h=10) |> boxplot()
abline(h=0, col="red2", lwd=2)

which will result in:

Distributions of the multistep forecast errors

The image above shows that the model tend to under shoot the actual values in-sample (because the boxplots tend to lie slightly above the zero line). This might cause a bias in the final forecasts.

The covariance matrix of the multistep forecast error looks like this in our case:

multicov(adamETSBJ, h=10) |> round(3)
       h1    h2     h3     h4     h5     h6     h7     h8     h9    h10
h1  1.918 2.299  2.860  3.299  3.643  3.911  4.121  4.286  4.414  4.515
h2  2.299 4.675  5.729  6.817  7.667  8.333  8.853  9.260  9.579  9.828
h3  2.860 5.729  8.942 10.651 12.250 13.501 14.480 15.246 15.845 16.314
h4  3.299 6.817 10.651 14.618 16.918 18.979 20.592 21.854 22.841 23.613
h5  3.643 7.667 12.250 16.918 21.538 24.348 26.808 28.733 30.239 31.417
h6  3.911 8.333 13.501 18.979 24.348 29.515 32.753 35.549 37.737 39.448
h7  4.121 8.853 14.480 20.592 26.808 32.753 38.372 41.964 45.036 47.440
h8  4.286 9.260 15.246 21.854 28.733 35.549 41.964 47.950 51.830 55.127
h9  4.414 9.579 15.845 22.841 30.239 37.737 45.036 51.830 58.112 62.223
h10 4.515 9.828 16.314 23.613 31.417 39.448 47.440 55.127 62.223 68.742

This is not useful on its own, but can be used for some further derivations.

Note that the returned values by both rmultistep() and multicov() depend on the model's error type (see Section 11.2 for clarification).

Model diagnostics

The conventional plot() method applied to a model estimated using adam() can produce a variety of images for the visual model diagnostics. This is controlled by the which parameter (overall, 16 options). The documentation of the plot.smooth() contains the exhaustive list of options and Chapter 14 of the monograph shows how they can be used for model diagnostics. Here I only list several main ones:

• plot(ourModel, which=1) - actuals vs fitted values. Can be used for general diagnostics of the model. Ideally, all points should lie around the diagonal line;
• plot(ourModel, which=2) - standardised residuals vs fitted values. Useful for detecting potential outliers. Also accepts the level parameter, which regulates the width of the confidence bounds.
• plot(ourModel, which=4) - absolute residuals vs fitted, which can be used for detecting heteroscedasticity of the residuals;
• plot(ourModel, which=6) - QQ plot for the analysis of the distribution of the residuals. The specific figure changes for different distribution assumed in the model (see Section 11.1 for the supported ones);
• plot(ourModel, which=7) - actuals, fitted values and point forecasts over time. Useful for understanding how the model fits the data and what point forecast it produces;
• plot(ourModel, which=c(10,11)) - ACF and PACF of the residuals of the model to detect potentially missing AR/MA elements;
• plot(ourModel, which=12) - plot of the components of the model. In case of ETS, will show the time series decomposition based on it.

And here are four default plots for the model that we estimated earlier:

par(mfcol=c(2,2))
plot(adamETSBJ)

Diagnostic plots for the estimated model

Based on the plot above, we can conclude that the model fits the data fine, does not have apparent heteroscedasticity, but has several potential outliers, which can be explored to improve it. The outliers detection is done via the outlierdummy() method, the generic of which is implemented in the greybox package.

Other useful methods

There are many methods that are used by functions to extract some information about the model. I sometimes use them to simplify my coding routine. Here they are:

• lags() - returns lags of the model. Especially useful if you fit a multiple seasonal model;
• orders() - the vector of orders of the model. Mainly useful in case of ARIMA, which can have multiple seasonalities and p,d,q,P,D,Q orders;
• modelType() - the type of the model. In case with the one fitted above will return "AAdN". Can be useful to easily refit the similar model on the new data;
• modelName() - the name of the model. In case of the one we fitted above will return "ETS(AAdN)";
• nobs(), nparam(), nvariate() - number of in-sample observations, number of all estimated parameters and number of time series used in the model respectively. The latter one is developed mainly for the multivariate models, such as VAR and VETS (e.g. legion package in R);
• logLik() - extracts log-Likelihood of the model;
• AIC(), AICc(), BIC(), BICc() - extract respective information criteria;
• sigma() - returns the standard error of the residuals.

More specialised methods

One of the methods that can be useful for scenarios and artificial data generation is simulate(). It will take the structure and parameters of the estimated model and use them to generate time series, similar to the original one. This is discussed in Section 16.1 of the ADAM monograph.

Furthermore, smooth implements the scale model, discussed in Chapter 17, which allows modelling time varying scale of distribution. This is done via the sm() method (generic introduced in the greybox package), the output of which can then be merged with the original model via the implant() method.

For the same model that we used earlier, the scale model can be estimated this way:

adamETSBJSM < - sm(adamETSBJ)

This is how it looks:

plot(adamETSBJSM, 7)

Scale model for the ADAM ETS

In the plot above, the y-axis contains the squared residuals. The fact that the holdout sample contains a large increase in the error is expected, because that part corresponds to the forecast errors rather than residuals. It is added to the plot for completeness.

To use the scale model in forecasting, we should implant it in the location one, which can be done using the following command:

adamETSBJFull < - implant(location=adamETSBJ, scale=adamETSBJSM)

The resulting model will have fewer degrees of freedom (because the scale model estimated two parameters), but its prediction interval will now take the scale model into account, and will differ from the original. We will now take into account the time varying variance based on the more recent information instead of the averaged one across the whole time series. In our case, the forecasted variance is lower than the one we would obtain in case of the adamETSBJ model. This leads to the narrower prediction interval (you can produce them for both models and compare):

forecast(adamETSBJFull, h=10, interval="prediction") |> plot()

Forecast from the full ADAM, containing both location and scale parts

Conclusions

The methods discussed above give a bit of flexibility of how to model things and what tools to use. I hope this makes your life easier and that you won't need to spend time reading the source code, but instead can focus on forecasting and analytics with ADAM.

Message Methods for the smooth functions in R first appeared on Open Forecasting.