Tuning hyper-parameters might be the most tedious yet crucial in various machine learning algorithms, such as neural networks, svm, or boosting. The configuration of hyper-parameters not only impacts the computational efficiency of a learning algorithm but also determines its prediction accuracy.

Thus far, manual tuning and grid searching are still the most prevailing strategies. In the paper http://www.jmlr.org/papers/volume13/bergstra12a/bergstra12a.pdf, Bergstra and Bengio showed that the random search is more efficient in the hyper-parameter optimization than both the grid search and the manual tuning. Following the similar logic of the random search, a Sobol sequence is a series of quasi-random numbers designed to cover the space more evenly than uniform random numbers.

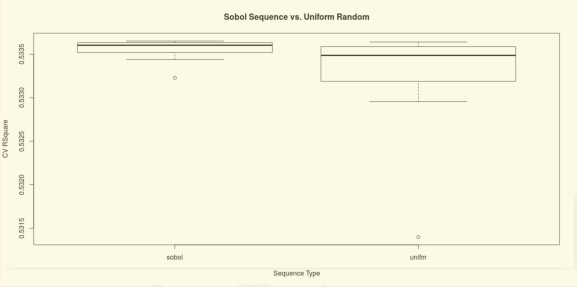
The demonstration below compared the Sobol sequence and the uniform random number generator in the hyper-parameter tuning of a General Regression Neural Network (GRNN). In this particular example, the Sobol sequence outperforms the uniform random number generator in two folds. First of all, it picks the hyper-parameter that yields a better performance, e.g. R^2, in the cross-validation. Secondly, the performance is more consistent in multiple trials with a lower variance.