Deep Learning from first principles in Python, R and Octave – Part 4

Posted on February 26, 2018 by Tinniam V Ganesh in R bloggers | 0 Comments

[This article was first published on R – Giga thoughts …, and kindly contributed to R-bloggers]. (You can report issue about the content on this page here)

Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.

In this 4th post of my series on Deep Learning from first principles in Python, R and Octave – Part 4, I explore the details of creating a multi-class classifier using the Softmax activation unit in a neural network. The earlier posts in this series were

1. Deep Learning from first principles in Python, R and Octave – Part 1. In this post I implemented logistic regression as a simple Neural Network in vectorized Python, R and Octave
2. Deep Learning from first principles in Python, R and Octave – Part 2. This 2nd part implemented the most elementary neural network with 1 hidden layer and any number of activation units in the hidden layer with sigmoid activation at the output layer
3. Deep Learning from first principles in Python, R and Octave – Part 3. The 3rd implemented a multi-layer Deep Learning network with an arbitrary number if hidden layers and activation units per hidden layer. The output layer was for binary classification which was based on the sigmoid unit. This multi-layer deep network was implemented in vectorized Python, R and Octave

This 4th part takes a swing at multi-class classification and uses the Softmax as the activation unit in the output layer. Inclusion of the Softmax activation unit in the activation layer requires us to compute the derivative of Softmax, or rather the “Jacobian” of the Softmax function, besides also computing the log loss for this Softmax activation during back propagation. Since the derivation of the Jacobian of a Softmax and the computation of the Cross Entropy/log loss is very involved, I have implemented a basic neural network with just 1 hidden layer with the Softmax activation at the output layer. I also perform multi-class classification based on the ‘spiral’ data set from CS231n Convolutional Neural Networks Stanford course, to test the performance and correctness of the implementations in Python, R and Octave. You can clone download the code for the Python, R and Octave implementations from Github at Deep Learning – Part 4

The Softmax function takes an N dimensional vector as input and generates a N dimensional vector as output.
The Softmax function is given by
$S_{j}= \frac{e_{j}}{\sum_{i}^{N}e_{k}}$
There is a probabilistic interpretation of the Softmax, since the sum of the Softmax values of a set of vectors will always add up to 1, given that each Softmax value is divided by the total of all values.

As mentioned earlier, the Softmax takes a vector input and returns a vector of outputs. For e.g. the Softmax of a vector a=[1, 3, 6] is another vector S=[0.0063,0.0471,0.9464]. Notice that vector output is proportional to the input vector. Also, taking the derivative of a vector by another vector, is known as the Jacobian. By the way, The Matrix Calculus You Need For Deep Learning by Terence Parr and Jeremy Howard, is very good paper that distills all the main mathematical concepts for Deep Learning in one place.

Let us take a simple 2 layered neural network with just 2 activation units in the hidden layer is shown below

$Z_{1}^{1} =W_{11}^{1}x_{1} + W_{21}^{1}x_{2} + b_{1}^{1}$
$Z_{2}^{1} =W_{12}^{1}x_{1} + W_{22}^{1}x_{2} + b_{2}^{1}$
and
$A_{1}^{1} = g'(Z_{1}^{1})$
$A_{2}^{1} = g'(Z_{2}^{1})$
where g'() is the activation unit in the hidden layer which can be a relu, sigmoid or a
tanh function

Note: The superscript denotes the layer. The above denotes the equation for layer 1
of the neural network. For layer 2 with the Softmax activation, the equations are
$Z_{1}^{2} =W_{11}^{2}x_{1} + W_{21}^{2}x_{2} + b_{1}^{2}$
$Z_{2}^{2} =W_{12}^{2}x_{1} + W_{22}^{2}x_{2} + b_{2}^{2}$
and
$A_{1}^{2} = S(A_{1}^{1})$
$A_{2}^{2} = S(A_{2}^{1})$
where S() is the Softmax activation function
$S=\begin{pmatrix} S(Z_{1}^{2})\\ S(Z_{2}^{2}) \end{pmatrix}$
$S=\begin{pmatrix} \frac{e^{Z1}}{e^{Z1}+e^{Z2}}\\ \frac{e^{Z2}}{e^{Z1}+e^{Z2}} \end{pmatrix}$

The Jacobian of the softmax ‘S’ is given by
$\begin{pmatrix} \frac {\partial S_{1}}{\partial Z_{1}} & \frac {\partial S_{1}}{\partial Z_{2}}\\ \frac {\partial S_{2}}{\partial Z_{1}} & \frac {\partial S_{2}}{\partial Z_{2}} \end{pmatrix}$
$\begin{pmatrix} \frac{\partial}{\partial Z_{1}} \frac {e^{Z1}}{e^{Z1}+ e^{Z2}} & \frac{\partial}{\partial Z_{2}} \frac {e^{Z1}}{e^{Z1}+ e^{Z2}}\\ \frac{\partial}{\partial Z_{1}} \frac {e^{Z2}}{e^{Z1}+ e^{Z2}} & \frac{\partial}{\partial Z_{2}} \frac {e^{Z2}}{e^{Z1}+ e^{Z2}} \end{pmatrix}$ – (A)

Now the ‘division-rule’ of derivatives is as follows. If u and v are functions of x, then
$\frac{d}{dx} \frac {u}{v} =\frac {vdu -udv}{v^{2}}$
Using this to compute each element of the above Jacobian matrix, we see that
when i=j we have
$\frac {\partial}{\partial Z1}\frac{e^{Z1}}{e^{Z1}+e^{Z2}} = \frac {\sum e^{Z1} - e^{Z1^{2}}}{\sum ^{2}}$
and when $i \neq j$
$\frac {\partial}{\partial Z1}\frac{e^{Z2}}{e^{Z1}+e^{Z2}} = \frac {0 - e^{z1}e^{Z2}}{\sum ^{2}}$
This is of the general form
$\frac {\partial S_{j}}{\partial z_{i}} = S_{i}( 1-S_{j})$ when i=j
and
$\frac {\partial S_{j}}{\partial z_{i}} = -S_{i}S_{j}$ when $i \neq j$
Note: Since the Softmax essentially gives the probability the following
notation is also used
$\frac {\partial p_{j}}{\partial z_{i}} = p_{i}( 1-p_{j})$ when i=j
and
$\frac {\partial p_{j}}{\partial z_{i}} = -p_{i}p_{j} when i \neq j$
If you throw the “Kronecker delta” into the equation, then the above equations can be expressed even more concisely as
$\frac {\partial p_{j}}{\partial z_{i}} = p_{i} (\delta_{ij} - p_{j})$
where $\delta_{ij} = 1$ when i=j and 0 when $i \neq j$

This reduces the Jacobian of the simple 2 output softmax vectors equation (A) as
$\begin{pmatrix} p_{1}(1-p_{1}) & -p_{1}p_{2} \\ -p_{2}p_{1} & p_{2}(1-p_{2}) \end{pmatrix}$
The loss of Softmax is given by
$L = -\sum y_{i} log(p_{i})$
For the 2 valued Softmax output this is
$\frac {dL}{dp1} = -\frac {y_{1}}{p_{1}}$
$\frac {dL}{dp2} = -\frac {y_{2}}{p_{2}}$
Using the chain rule we can write
$\frac {\partial L}{\partial w_{pq}} = \sum _{i}\frac {\partial L}{\partial p_{i}} \frac {\partial p_{i}}{\partial w_{pq}}$ (1)
and
$\frac {\partial p_{i}}{\partial w_{pq}} = \sum _{k}\frac {\partial p_{i}}{\partial z_{k}} \frac {\partial z_{k}}{\partial w_{pq}}$ (2)
In expanded form this is
$\frac {\partial L}{\partial w_{pq}} = \sum _{i}\frac {\partial L}{\partial p_{i}} \sum _{k}\frac {\partial p_{i}}{\partial z_{k}} \frac {\partial z_{k}}{\partial w_{pq}}$
Also
$\frac {\partial L}{\partial Z_{i}} =\sum _{i} \frac {\partial L}{\partial p} \frac {\partial p}{\partial Z_{i}}$
Therefore
$\frac {\partial L}{\partial Z_{1}} =\frac {\partial L}{\partial p_{1}} \frac {\partial p_{1}}{\partial Z_{1}} +\frac {\partial L}{\partial p_{2}} \frac {\partial p_{2}}{\partial Z_{1}}$
$\frac {\partial L}{\partial z_{1}}=-\frac {y1}{p1} p1(1-p1) - \frac {y2}{p2}*(-p_{2}p_{1})$
Since
$\frac {\partial p_{j}}{\partial z_{i}} = p_{i}( 1-p_{j})$ when i=j
and
$\frac {\partial p_{j}}{\partial z_{i}} = -p_{i}p_{j}$ when $i \neq j$
which simplifies to
$\frac {\partial L}{\partial Z_{1}} = -y_{1} + y_{1}p_{1} + y_{2}p_{1} =$
$p_{1}\sum (y_{1} + y_2) - y_{1}$
$\frac {\partial L}{\partial Z_{1}}= p_{1} - y_{1}$
Since
$\sum_{i} y_{i} =1$
Similarly
$\frac {\partial L}{\partial Z_{2}} =\frac {\partial L}{\partial p_{1}} \frac {\partial p_{1}}{\partial Z_{2}} +\frac {\partial L}{\partial p_{2}} \frac {\partial p_{2}}{\partial Z_{2}}$
$\frac {\partial L}{\partial z_{2}}=-\frac {y1}{p1}*(p_{1}p_{2}) - \frac {y2}{p2}*p_{2}(1-p_{2})$
$y_{1}p_{2} + y_{2}p_{2} - y_{2}$
$\frac {\partial L}{\partial Z_{2}} =p_{2}\sum (y_{1} + y_2) - y_{2}\\ = p_{2} - y_{2}$
In general this is of the form
$\frac {\partial L}{\partial z_{i}} = p_{i} -y_{i}$
For e.g if the probabilities computed were p=[0.1, 0.7, 0.2] then this implies that the class with probability 0.7 is the likely class. This would imply that the ‘One hot encoding’ for yi would be yi=[0,1,0] therefore the gradient pi-yi = [0.1,-0.3,0.2]

Note: Further, we could extend this derivation for a Softmax activation output that outputs 3 classes
$S=\begin{pmatrix} \frac{e^{z1}}{e^{z1}+e^{z2}+e^{z3}}\\ \frac{e^{z2}}{e^{z1}+e^{z2}+e^{z3}} \\ \frac{e^{z3}}{e^{z1}+e^{z2}+e^{z3}} \end{pmatrix}$

We could derive
$\frac {\partial L}{\partial z1}= \frac {\partial L}{\partial p_{1}} \frac {\partial p_{1}}{\partial z_{1}} +\frac {\partial L}{\partial p_{2}} \frac {\partial p_{2}}{\partial z_{1}} +\frac {\partial L}{\partial p_{3}} \frac {\partial p_{3}}{\partial z_{1}}$ which similarly reduces to
$\frac {\partial L}{\partial z_{1}}=-\frac {y1}{p1} p1(1-p1) - \frac {y2}{p2}*(-p_{2}p_{1}) - \frac {y3}{p3}*(-p_{3}p_{1})$
$-y_{1}+ y_{1}p_{1} + y_{2}p_{1} + y_{3}p1 = p_{1}\sum (y_{1} + y_2 + y_3) - y_{1} = p_{1} - y_{1}$
Interestingly, despite the lengthy derivations the final result is simple and intuitive!

As seen in my post ‘Deep Learning from first principles with Python, R and Octave – Part 3 the key equations for forward and backward propagation are

Forward propagation equations layer 1
$Z_{1} = W_{1}X +b_{1}$ and $A_{1} = g(Z_{1})$
Forward propagation equations layer 1
$Z_{2} = W_{2}A_{1} +b_{2}$ and $A_{2} = S(Z_{2})$

Backward propagation equations layer 2
$\partial L/\partial W_{2} =\partial L/\partial Z_{2} *A_{1}$
$\partial L/\partial b_{2} =\partial L/\partial Z_{2}$
$\partial L/\partial A_{1} = \partial L/\partial Z_{2} * W_{2}$
Backward propagation equations layer 1
$\partial L/\partial W_{1} =\partial L/\partial Z_{1} *A_{0}$
$\partial L/\partial b_{1} =\partial L/\partial Z_{2}$

2.0 Spiral data set

As I mentioned earlier, I will be using the ‘spiral’ data from CS231n Convolutional Neural Networks to ensure that my vectorized implementations in Python, R and Octave are correct. Here is the ‘spiral’ data set.

import numpy as np import matplotlib.pyplot as plt import os os.chdir("C:/junk/dl-4/dl-4") exec(open("././DLfunctions41.py").read()) # Create an input data set - Taken from CS231n Convolutional Neural networks # http://cs231n.github.io/neural-networks-case-study/ N = 100 # number of points per class D = 2 # dimensionality K = 3 # number of classes X = np.zeros((N*K,D)) # data matrix (each row = single example) y = np.zeros(N*K, dtype='uint8') # class labels for j in range(K): ix = range(N*j,N*(j+1)) r = np.linspace(0.0,1,N) # radius t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta X[ix] = np.c_[r*np.sin(t), r*np.cos(t)] y[ix] = j # Plot the data plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral) plt.savefig("fig1.png", bbox_inches='tight')

The implementations of the vectorized Python, R and Octave code are shown diagrammatically below

2.1 Multi-class classification with Softmax – Python code

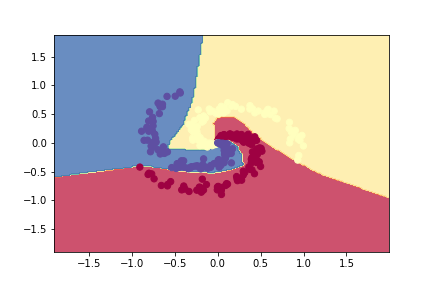
A simple 2 layer Neural network with a single hidden layer , with 100 Relu activation units in the hidden layer and the Softmax activation unit in the output layer is used for multi-class classification. This Deep Learning Network, plots the non-linear boundary of the 3 classes as shown below

import numpy as np import matplotlib.pyplot as plt import os os.chdir("C:/junk/dl-4/dl-4") exec(open("././DLfunctions41.py").read()) # Read the input data N = 100 # number of points per class D = 2 # dimensionality K = 3 # number of classes X = np.zeros((N*K,D)) # data matrix (each row = single example) y = np.zeros(N*K, dtype='uint8') # class labels for j in range(K): ix = range(N*j,N*(j+1)) r = np.linspace(0.0,1,N) # radius t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta X[ix] = np.c_[r*np.sin(t), r*np.cos(t)] y[ix] = j # Set the number of features, hidden units in hidden layer and number of classess numHidden=100 # No of hidden units in hidden layer numFeats= 2 # dimensionality numOutput = 3 # number of classes # Initialize the model parameters=initializeModel(numFeats,numHidden,numOutput) W1= parameters['W1'] b1= parameters['b1'] W2= parameters['W2'] b2= parameters['b2'] # Set the learning rate learningRate=0.6 # Initialize losses losses=[] # Perform Gradient descent for i in range(10000): # Forward propagation through hidden layer with Relu units A1,cache1= layerActivationForward(X.T,W1,b1,'relu') # Forward propagation through output layer with Softmax A2,cache2 = layerActivationForward(A1,W2,b2,'softmax') # No of training examples numTraining = X.shape[0] # Compute log probs. Take the log prob of correct class based on output y correct_logprobs = -np.log(A2[range(numTraining),y]) # Conpute loss loss = np.sum(correct_logprobs)/numTraining # Print the loss if i % 1000 == 0: print("iteration %d: loss %f" % (i, loss)) losses.append(loss) dA=0 # Backward propagation through output layer with Softmax dA1,dW2,db2 = layerActivationBackward(dA, cache2, y, activationFunc='softmax') # Backward propagation through hidden layer with Relu unit dA0,dW1,db1 = layerActivationBackward(dA1.T, cache1, y, activationFunc='relu') #Update paramaters with the learning rate W1 += -learningRate * dW1 b1 += -learningRate * db1 W2 += -learningRate * dW2.T b2 += -learningRate * db2.T #Plot losses vs iterations i=np.arange(0,10000,1000) plt.plot(i,losses) plt.xlabel('Iterations') plt.ylabel('Loss') plt.title('Losses vs Iterations') plt.savefig("fig2.png", bbox="tight") #Compute the multi-class Confusion Matrix from sklearn.metrics import confusion_matrix from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score # We need to determine the predicted values from the learnt data # Forward propagation through hidden layer with Relu units A1,cache1= layerActivationForward(X.T,W1,b1,'relu') # Forward propagation through output layer with Softmax A2,cache2 = layerActivationForward(A1,W2,b2,'softmax') #Compute predicted values from weights and biases yhat=np.argmax(A2, axis=1) a=confusion_matrix(y.T,yhat.T) print("Multi-class Confusion Matrix") print(a) ## iteration 0: loss 1.098507 ## iteration 1000: loss 0.214611 ## iteration 2000: loss 0.043622 ## iteration 3000: loss 0.032525 ## iteration 4000: loss 0.025108 ## iteration 5000: loss 0.021365 ## iteration 6000: loss 0.019046 ## iteration 7000: loss 0.017475 ## iteration 8000: loss 0.016359 ## iteration 9000: loss 0.015703 ## Multi-class Confusion Matrix ## [[ 99 1 0] ## [ 0 100 0] ## [ 0 1 99]]

To know more details about Confusion Matrix and other related measures check out my book My book ‘Practical Machine Learning with R and Python’ on Amazon

2.2 Multi-class classification with Softmax – R code

The spiral data set created with Python was saved, and is used as the input with R code. The R Neural Network seems to perform much,much slower than both Python and Octave. Not sure why! Incidentally the computation of loss and the softmax derivative are identical for both R and Octave. yet R is much slower. To compute the softmax derivative I create matrices for the One Hot Encoded yi and then stack them before subtracting pi-yi. I am sure there is a more elegant and more efficient way to do this, much like Python. Any suggestions?

library(ggplot2) library(dplyr) library(RColorBrewer) source("DLfunctions41.R") # Read the spiral dataset Z <- as.matrix(read.csv("spiral.csv",header=FALSE)) Z1=data.frame(Z) #Plot the dataset ggplot(Z1,aes(x=V1,y=V2,col=V3)) +geom_point() + scale_colour_gradientn(colours = brewer.pal(10, "Spectral"))

# Setup the data X <- Z[,1:2] y <- Z[,3] X1 <- t(X) Y1 <- t(y) # Initialize number of features, number of hidden units in hidden layer and # number of classes numFeats<-2 # No features numHidden<-100 # No of hidden units numOutput<-3 # No of classes # Initialize model parameters <-initializeModel(numFeats, numHidden,numOutput) W1 <-parameters[['W1']] b1 <-parameters[['b1']] W2 <-parameters[['W2']] b2 <-parameters[['b2']] # Set the learning rate learningRate <- 0.5 # Initialize losses losses <- NULL # Perform gradient descent for(i in 0:9000){ # Forward propagation through hidden layer with Relu units retvals <- layerActivationForward(X1,W1,b1,'relu') A1 <- retvals[['A']] cache1 <- retvals[['cache']] forward_cache1 <- cache1[['forward_cache1']] activation_cache <- cache1[['activation_cache']] # Forward propagation through output layer with Softmax units retvals = layerActivationForward(A1,W2,b2,'softmax') A2 <- retvals[['A']] cache2 <- retvals[['cache']] forward_cache2 <- cache2[['forward_cache1']] activation_cache2 <- cache2[['activation_cache']] # No oftraining examples numTraining <- dim(X)[1] dA <-0 # Select the elements where the y values are 0, 1 or 2 and make a vector a=c(A2[y==0,1],A2[y==1,2],A2[y==2,3]) # Take log correct_probs = -log(a) # Compute loss loss= sum(correct_probs)/numTraining if(i %% 1000 == 0){ sprintf("iteration %d: loss %f",i, loss) print(loss) } # Backward propagation through output layer with Softmax units retvals = layerActivationBackward(dA, cache2, y, activationFunc='softmax') dA1 = retvals[['dA_prev']] dW2= retvals[['dW']] db2= retvals[['db']] # Backward propagation through hidden layer with Relu units retvals = layerActivationBackward(t(dA1), cache1, y, activationFunc='relu') dA0 = retvals[['dA_prev']] dW1= retvals[['dW']] db1= retvals[['db']] # Update parameters W1 <- W1 - learningRate * dW1 b1 <- b1 - learningRate * db1 W2 <- W2 - learningRate * t(dW2) b2 <- b2 - learningRate * t(db2) } ## [1] 1.212487 ## [1] 0.5740867 ## [1] 0.4048824 ## [1] 0.3561941 ## [1] 0.2509576 ## [1] 0.7351063 ## [1] 0.2066114 ## [1] 0.2065875 ## [1] 0.2151943 ## [1] 0.1318807

#Create iterations iterations <- seq(0,10) #df=data.frame(iterations,losses) ggplot(df,aes(x=iterations,y=losses)) + geom_point() + geom_line(color="blue") + ggtitle("Losses vs iterations") + xlab("Iterations") + ylab("Loss") plotDecisionBoundary(Z,W1,b1,W2,b2)

Multi-class Confusion Matrix

library(caret) library(e1071) # Forward propagation through hidden layer with Relu units retvals <- layerActivationForward(X1,W1,b1,'relu') A1 <- retvals[['A']] # Forward propagation through output layer with Softmax units retvals = layerActivationForward(A1,W2,b2,'softmax') A2 <- retvals[['A']] yhat <- apply(A2, 1,which.max) -1 Confusion Matrix and Statistics Reference Prediction 0 1 2 0 97 0 1 1 2 96 4 2 1 4 95 Overall Statistics Accuracy : 0.96 95% CI : (0.9312, 0.9792) No Information Rate : 0.3333 P-Value [Acc > NIR] : <2e-16 Kappa : 0.94 Mcnemar's Test P-Value : 0.5724 Statistics by Class: Class: 0 Class: 1 Class: 2 Sensitivity 0.9700 0.9600 0.9500 Specificity 0.9950 0.9700 0.9750 Pos Pred Value 0.9898 0.9412 0.9500 Neg Pred Value 0.9851 0.9798 0.9750 Prevalence 0.3333 0.3333 0.3333 Detection Rate 0.3233 0.3200 0.3167 Detection Prevalence 0.3267 0.3400 0.3333 Balanced Accuracy 0.9825 0.9650 0.9625

My book “Practical Machine Learning with R and Python” includes the implementation for many Machine Learning algorithms and associated metrics. Pick up your copy today!

2.3 Multi-class classification with Softmax – Octave code

A 2 layer Neural network with the Softmax activation unit in the output layer is constructed in Octave. The same spiral data set is used for Octave also
source("DL41functions.m") # Read the spiral data data=csvread("spiral.csv"); # Setup the data X=data(:,1:2); Y=data(:,3); # Set the number of features, number of hidden units in hidden layer and number of classes numFeats=2; #No features numHidden=100; # No of hidden units numOutput=3; # No of classes # Initialize model [W1 b1 W2 b2] = initializeModel(numFeats,numHidden,numOutput); # Initialize losses losses=[] #Initialize learningRate learningRate=0.5; for k =1:10000 # Forward propagation through hidden layer with Relu units [A1,cache1 activation_cache1]= layerActivationForward(X',W1,b1,activationFunc ='relu'); # Forward propagation through output layer with Softmax units [A2,cache2 activation_cache2] = layerActivationForward(A1,W2,b2,activationFunc='softmax'); # No of training examples numTraining = size(X)(1); # Select rows where Y=0,1,and 2 and concatenate to a long vector a=[A2(Y==0,1) ;A2(Y==1,2) ;A2(Y==2,3)]; #Select the correct column for log prob correct_probs = -log(a); #Compute log loss loss= sum(correct_probs)/numTraining; if(mod(k,1000) == 0) disp(loss); losses=[losses loss]; endif dA=0; # Backward propagation through output layer with Softmax units [dA1 dW2 db2] = layerActivationBackward(dA, cache2, activation_cache2,Y,activationFunc='softmax'); # Backward propagation through hidden layer with Relu units [dA0,dW1,db1] = layerActivationBackward(dA1', cache1, activation_cache1, Y, activationFunc='relu'); #Update parameters W1 += -learningRate * dW1; b1 += -learningRate * db1; W2 += -learningRate * dW2'; b2 += -learningRate * db2'; endfor # Plot Losses vs Iterations iterations=0:1000:9000 plotCostVsIterations(iterations,losses) # Plot the decision boundary plotDecisionBoundary( X,Y,W1,b1,W2,b2)

The code for the Python, R and Octave implementations can be downloaded from Github at Deep Learning – Part 4

Conclusion

In this post I have implemented a 2 layer Neural Network with the Softmax classifier. In Part 3, I implemented a multi-layer Deep Learning Network. I intend to include the Softmax activation unit into the generalized multi-layer Deep Network along with the other activation units of sigmoid,tanh and relu.

Stick around, I’ll be back!!
Watch this space!

References
1. Deep Learning Specialization
2. Neural Networks for Machine Learning
3. CS231 Convolutional Neural Networks for Visual Recognition
4. Eli Bendersky’s Website – The Softmax function and its derivative
5. Cross Validated – Backpropagation with Softmax / Cross Entropy
6. Stackoverflow – CS231n: How to calculate gradient for Softmax loss function?
7. Math Stack Exchange – Derivative of Softmax
8. The Matrix Calculus for Deep Learning

You may like
1.My book ‘Practical Machine Learning with R and Python’ on Amazon
2. My travels through the realms of Data Science, Machine Learning, Deep Learning and (AI)
3. Deblurring with OpenCV: Weiner filter reloaded
4. A method to crowd source pothole marking on (Indian) roads
5. Rock N’ Roll with Bluemix, Cloudant & NodeExpress
6. Sea shells on the seashore
7. Design Principles of Scalable, Distributed Systems

To see all post click Index of posts

Related

Share Tweet

To leave a comment for the author, please follow the link and comment on their blog: R – Giga thoughts ….

R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.