Interaction are the funny interesting part of ecology, the most fun during data analysis is when you try to understand and to derive explanations from the estimated coefficients of your model. However you do need to know what is behind these estimate, there is a mathematical foundation between them that you need to be aware of before being able to derive explanations.

I plan to make two post on this issue, this first one will deal with interpreting interactions coefficients from classical linear models, a second one will look at the F-ratios of these coefficients and what they mean. I will only look at two-way interaction because above this my brain start to collapse. Some later one might be taking into account the extensive litterature on these issues that I only started to scratch.

So this post is divided in three parts: i) interaction between two categorical variables, ii) interaction between one continuous and one categorical variables and finally iii) interaction between two continuous variables.

If you want to have a look at a clean page with code/figures go there: http://rpubs.com/hughes/15353

i) Interaction between two categorical variables:

Let’s make an hypothetical examples of a study, we measured the shoot length of some plant species under two different treatments: one is with increasing temperature (Low, High), the other is with three levels of nitrogen addition (A, B, C). We have made a completely factorial design and would like to look at the effect of these two treatments and their interactions on the shoot length.

# interpreting interaction coefficients from lm first case two categorical
# variables
set.seed(12)
f1 <- gl(n = 2, k = 30, labels = c("Low", "High"))
f2 <- as.factor(rep(c("A", "B", "C"), times = 20))
modmat <- model.matrix(~f1 * f2, data.frame(f1 = f1, f2 = f2))
coeff <- c(1, 3, -2, -4, 1, -1.2)
y <- rnorm(n = 60, mean = modmat %*% coeff, sd = 0.1)
dat <- data.frame(y = y, f1 = f1, f2 = f2)
summary(lm(y ~ f1 * f2))


## 
## Call:
## lm(formula = y ~ f1 * f2)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.19948 -0.06375 -0.00109  0.05816  0.22223 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   0.9785     0.0287    34.1   <2e-16 ***
## f1High        3.0031     0.0405    74.1   <2e-16 ***
## f2B          -1.9788     0.0405   -48.8   <2e-16 ***
## f2C          -4.0021     0.0405   -98.8   <2e-16 ***
## f1High:f2B    0.9892     0.0573    17.3   <2e-16 ***
## f1High:f2C   -1.1662     0.0573   -20.4   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.0906 on 54 degrees of freedom
## Multiple R-squared:  0.999,  Adjusted R-squared:  0.999 
## F-statistic: 8.78e+03 on 5 and 54 DF,  p-value: <2e-16

The first coefficient (0.97) is the intercept, so the shoot length for the Low temperature and the A nitrogen addition treatment. The second one (3) is the difference between the mean shoot length of the High temperature and the Low temperature treatment. Similarly the third and fourth one (-1.97, 4) are the mean shoot length difference between the treatment B-A and between the treatment C-A. The fifth and sixth one are more tricky, they are the added mean shoot length for pots with temperature High and nitrogen addition B or C as compared to the intercept. For example to get the mean shoot length for High temperature and nitrogen B we do: 0.97+3-1.97+0.98, this 0.98 is then the added difference for tese particular cases.

So in this context the interaction coefficient cannot be interpreted alone, we need to look at the other main effects coefficient to understand their effects.

ii) Interaction between one continuous and one categorical variables

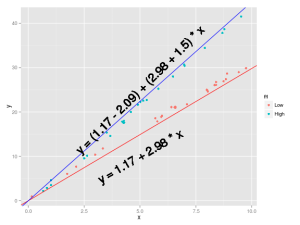
Now let’s turn to another case, there we are weighting standardize soil samples, we added a temperature treatment with two levels (Low, High) and we measured the soil nitrogen concentration, we would like to see the effects of the nitrogen concentration and its interaction with temperature on soil weight.

# second case one categorical and one continuous variable
x <- runif(50, 0, 10)
f1 <- gl(n = 2, k = 25, labels = c("Low", "High"))
modmat <- model.matrix(~x * f1, data.frame(f1 = f1, x = x))
coeff <- c(1, 3, -2, 1.5)
y <- rnorm(n = 50, mean = modmat %*% coeff, sd = 0.5)
dat <- data.frame(y = y, f1 = f1, x = x)
summary(lm(y ~ x * f1))
## 
## Call:
## lm(formula = y ~ x * f1)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.9222 -0.2663 -0.0347  0.3586  1.0077 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   1.1713     0.2621    4.47  5.1e-05 ***
## x             2.9876     0.0377   79.20  < 2e-16 ***
## f1High       -2.0925     0.3338   -6.27  1.1e-07 ***
## x:f1High      1.4924     0.0539   27.67  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.476 on 46 degrees of freedom
## Multiple R-squared:  0.998,  Adjusted R-squared:  0.998 
## F-statistic: 6.59e+03 on 3 and 46 DF,  p-value: <2e-16

This is an easy case, the first coefficient is the intercept, the second is the slope between the weight and the soil nitrogen concentration, the third one is the difference when the nitrogen concentration is 0 between the means for the two temperature treatments, and the fourth is the change in the slope weight~nitrogen between the Low and High temperature treatment.

iii) Interaction between two continuous variables

Now the last possible case could be something like a study where we measured the attack rates of carabids beetles on some prey and we collected two continuous variable: the number of prey item in the proximity of the beetles and the air temperature. We would like to see how these two variables influence the attack rates

# third case interaction between two continuous variables
x1 <- runif(50, 0, 10)
x2 <- rnorm(50, 10, 3)
modmat <- model.matrix(~x1 * x2, data.frame(x1 = x1, x2 = x2))
coeff <- c(1, 2, -1, 1.5)
y <- rnorm(50, mean = modmat %*% coeff, sd = 0.5)
dat <- data.frame(y = y, x1 = x1, x2 = x2)
summary(lm(y ~ x1 * x2))

## 
## Call:
## lm(formula = y ~ x1 * x2)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.8202 -0.2755 -0.0405  0.2214  0.8711 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   0.7847     0.4038    1.94    0.058 .  
## x1            2.0076     0.0639   31.41   <2e-16 ***
## x2           -0.9810     0.0385  -25.48   <2e-16 ***
## x1:x2         1.4997     0.0063  237.95   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.421 on 46 degrees of freedom
## Multiple R-squared:     1,   Adjusted R-squared:     1 
## F-statistic: 2.64e+05 on 3 and 46 DF,  p-value: <2e-16

In this case we have to be carefull, the first coefficient as always is the intercept, the second one is the slope between the attack rates and the number of prey when the temperature is equal to 0, the third one is the slope between the attack rates and the temperature when the number of preys is equal to 0, the fourt one is the change in the slope as on of the two variables increases, for eaxmple if the number of prey items increase by one the slope between the attack rates and the temperature increase by 1.49 in this case. If the two variables can never reach 0 (ie when measuring length) then the interpretation of the second and third coefficient is useless and the variables should be centered around 0 for them to be safely interpreted. Now we can plot the relation between the attack rates and the temperature for different values of the number of preys:

So next time we will look at how to interprete the sum of squares of these interactions terms from anova output.

Happy conding.