I am looking at the following tickers from 2005-01-01 to 2008-01-01. The tickers are GE, F, MSFT, DELL, INTC. I will find the mean-variance weights and the R-ratio weights and then test portfolio performance from 2008-01-01 to 2010-01-01. This is a pretty limited test as the portfolio weights will be static over the test period, which is very unrealistic. But it still will give us a general idea of the relative performance of each optimization technique in case of extreme events (2008 crisis in this case).

Using the procedures I went over in my previous posts I obtained the following weights for each technique:

Mean-Variance: GE-19.8%   F-0%   MSFT-70.4%  DELL-0%   INTC-9.8%

R-ratio: GE-80.3%   F-0.7%   MSFT-14%   DELL-0%   INTC-5%

These are the results for the mean-variance portfolio from 2005-01-01 to 2008-01-01

Cumulative Return: 0.25507335    Annual Return: 0.07888944

Annualized Sharpe Ratio: 0.47503374  Win %: 0.51128818

Annualized Volatility: 0.16607124     Maximum Drawdown: -0.21479303

Max Length Drawdown: 236.00000000
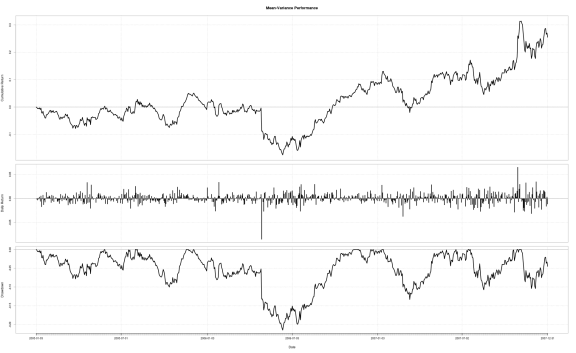And this is how the mean-variance portfolio did from 2008-01-01 to 2010-01-01:

Cumulative Return: -0.3332456    Annual Return: -0.1831219

Annualized Sharpe Ratio: -0.4551308  Win %: 0.5039683

Annualized Volatility: 0.4023501   Maximum Drawdown: -0.6618125

Max Length Drawdown: 504.0000000

Now, moving on to returns from the r-ratio portfolio from 2005-01-01 to 2008-01-01:

Cumulative Return: 0.10471265    Annual Return: 0.03384322

Annualized Sharpe Ratio: 0.23811103 Win %: 0.50464807

Annualized Volatility: 0.14213208   Maximum Drawdown: -0.13000366

Max Length Drawdown: 345.00000000

And from 2008-01-01 to 2010-01-01

Cumulative Return: -0.5929209 Annual Return: -0.3614045

Annualized Sharpe Ratio: -0.7272896  Win %: 0.4920635

Annualized Volatility: 0.4969197   Maximum Drawdown: -0.8058170

Max Length Drawdown: 444.0000000

Very interesting results. The R-ratio portfolio performed substantially worse than the minimum-variance portfolio, contrary to my original hypothesis. This may well be due to the very small size of the portfolio we were testing, leaving it vulnerable to idiosyncratic risk. For more robust results, I will need to run these tests on portfolios of much greater size to wash out idiosyncratic risk. I will need to conduct this test on various portfolios of a fixed size (number of securities and market cap) to get a broader understanding of the variation in performance between the two optimization techniques.

It could also be that the distribution of the securities changed, rendering the CVaR values used to calculate the R-ratio wrong. In fact, we would expect the distributions to change, given the magnitude of the events which occurred in 2008 (and how far out in the tails they were considered to be).