It is officially no longer pi day, but I didn’t see this Drew Conway post about estimating pi until just a few minutes ago. Because Google Reader doesn’t show github embeds, I also got to try it without seeing Drew’s solution. The estimation method relies on exploiting the area of a circle.

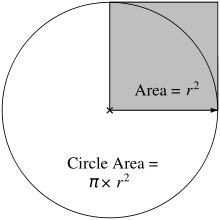
We can use R to generate random numbers for our and coordinates and count up the number of pairs inside the circle (or quarter of a circle, in our case). Because is the area of our quarter circle, the ratio of the 4 times the number of random coordinates within the quarter circle to the total number of random coordinates should converge on . This is a very simple Monte Carlo integration. So what do we get?

From pi day

Gets pretty close! The final error was , not too shabby! I’m computing the running sample average, so it isn’t a true Monte Carlo, but it converges well enough. Code is below: